Question

A 2.0 kg block is held at rest against a spring with a force constant k = 264 N/m. The spring is compressed a certain distance and then the block is released. When the block is released, it slides across a surface that has no friction except for a 10.0 cm section that has a coefficient of friction μk = 0.54.

Find the distance in centimeters the spring was compressed such that the block's speed after crossing the rough area is 2.7 m/s.

Answer 1

21.73 cm

Step-by-step explanation:

We have given parameters:

Mass of block, m = 2.0 kg

Force constant of spring, k = 264 N/m

Length of rough area, L = 10 cm = 0.1 m

Co-efficient of kinetic friction ,
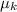`\mu_(k)` = 0.54

Block's speed after crossing rough area, v = 2.7 m/s

Block's initial speed ( when it was released from compressed spring),
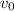`v_(0)` = 0 m/s

We need to find the distance that the spring was initially compressed, x = ?

Hence, we well apply Work-Energy principle which indicates that,

Work done by the friction = Change in the total energy of block

`- \mu_(k) * mg * L = ((1)/(2) * mv^(2) - (1)/(2) * mv_(0) ^(2) ) + (0 - (1)/(2) * kx^(2))`

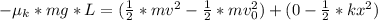
-0.54 * 2 * 9.8 * 0.1 = (1/2 * 2 *
`2.7^(2)` - 1/2 * 2 * 0) + (0 - 1/2 * 264 *
`x^(2)`)

x = 0.2173 m = 21.73 cm