Question

What is the twentieth term of the arithmetic sequence 21, 18, 15, 12, ... ?

78

-39

-36

1

Answer 1

Option (C).

The twentieth term of the given arithmetic sequence is -36.

Explanation:

The given arithmetic sequence is,

21, 18, 15, 12, ...........

Now, the first term of the arithmetic sequence, a₁ = 21

Second term of the arithmetic sequence, a₂ = 18

Third term of the arithmetic sequence, a₃ = 15

Fourth term of the arithmetic sequence, a₄ = 12

and so on.

Now, common difference, d = a₂ - a₁ = 18 - 21 = -3

We know that,
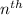`n^(th)` term of an arithmetic sequence is given by,

aₙ = a₁ + (n - 1)d

To find the
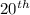`20^(th)` term of the given arithmetic sequence, we will substitute the values of a₁ , n and d in the above expression of aₙ.

Put a₁ = 21; n = 20 and d = -3 in the above expression of aₙ, we get

`a_(20)=21+(20-1)(-3)=21+19*(-3)=21-57=-36`

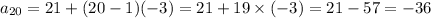
So, twentieth term of the given arithmetic sequence is -36.

Hence, option (C) is the correct answer.