Question

Many people believe that the daily change of price of a company's stock on the stock market is a random variable with mean 0 and variance 2. That is, if Yn represents the price of the stock on the n-th day, then Yn = Yn-1 + Xn, n > 1 where X1, X2, . . . are independent and identically distributed random variables with mean 0 and variance 2. Suppose that the stock's price today is 100. If 2 = 1, use CLT to approximate the probability that the stock's price will exceed 105 on the 10-th day?

Answer 1

Explanation:

We can use normal aproximation, assuming that the random variables are a lot of that means the sample size is large.

`P(x>105) = P(z>(105-100)/(1))=P(z>5)`

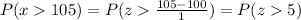
Using the normal distribution table,

P(z>5) = 0.00005

Hence, we can conclude that the probability that the stock’s price will exceed 105 after 10 days is very small.

Hope this helps!