Question

Is education related to programming preference when watching TV? From a poll of 80 television viewers, the following data have been collected: Level of Education Preferred TV stations High School Some college Bachelor’s degree or higher Total Public Broadcasting 15 15 10 40 Commercial Stations 5 25 10 40 Total 20 40 20 80 Test the null hypothesis that there is no association between level of education and TV station preference. A. State the null and alternative hypotheses. B. Calculate a test statistic, C. At the .05 level of significance, state the critical value, D. State your decision and conclusion.

Answer 1

a) H0: There is no association between level of education and TV station preference (Independence)

H1: There is association between level of education and TV station preference (No independence)

b)
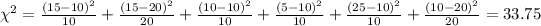
`\chi^2 = ((15-10)^2)/(10)+((15-20)^2)/(20)+((10-10)^2)/(10)+((5-10)^2)/(10)+((25-10)^2)/(10)+((10-20)^2)/(20) =33.75`

c)
`\chi^2_(crit)=5.991`

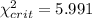
d) Since the p value is lower than the significance level we enough evidence to reject the null hypothesis at 5% of significance, and we can conclude that we have dependence between the two variables analyzed.

Explanation:

A chi-square goodness of fit test "determines if a sample data matches a population".

A chi-square test for independence "compares two variables in a contingency table to see if they are related. In a more general sense, it tests to see whether distributions of categorical variables differ from each another".

Assume the following dataset:

High school Some College Bachelor or higher Total

Public Broadcasting 15 15 10 40

Commercial stations 5 25 10 40

Total 20 40 20 80

We need to conduct a chi square test in order to check the following hypothesis:

Part a

H0: There is no association between level of education and TV station preference (Independence)

H1: There is association between level of education and TV station preference (No independence)

The level os significance assumed for this case is
`\alpha=0.05`

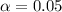
The statistic to check the hypothesis is given by:

`\sum_(i=1)^n ((O_i -E_i)^2)/(E_i)`

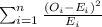
Part b

The table given represent the observed values, we just need to calculate the expected values with the following formula
`E_i = (total col * total row)/(grand total)`

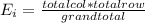
And the calculations are given by:

`E_(1) =(20*40)/(80)=10`

`E_(2) =(40*40)/(80)=20`

`E_(3) =(20*40)/(80)=10`

`E_(4) =(20*40)/(80)=10`

`E_(5) =(40*40)/(80)=20`

`E_(6) =(20*40)/(80)=10`

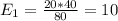
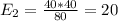
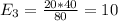
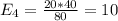
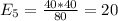
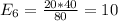
And the expected values are given by:

High school Some College Bachelor or higher Total

Public Broadcasting 10 20 10 40

Commercial stations 10 10 20 40

Total 20 30 30 80

Part b

And now we can calculate the statistic:

`\chi^2 = ((15-10)^2)/(10)+((15-20)^2)/(20)+((10-10)^2)/(10)+((5-10)^2)/(10)+((25-10)^2)/(10)+((10-20)^2)/(20) =33.75`

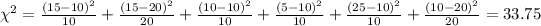
Now we can calculate the degrees of freedom for the statistic given by:

`df=(rows-1)(cols-1)=(2-1)(3-1)=2`

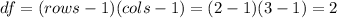
Part c

In order to find the critical value we need to look on the right tail of the chi square distribution with 2 degrees of freedom a value that accumulates 0.05 of the area. And this value is
`\chi^2_(crit)=5.991`

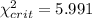
Part d

And we can calculate the p value given by:

`p_v = P(\chi^2_(3) >33.75)=2.23x10^(-7)`

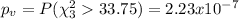
And we can find the p value using the following excel code:

"=1-CHISQ.DIST(33.75,2,TRUE)"

Since the p value is lower than the significance level we enough evidence to reject the null hypothesis at 5% of significance, and we can conclude that we have dependence between the two variables analyzed.