Answer:
b. -11.6 cm
Step-by-step explanation:
We have given parameters:
Length, l = 1.5 m = 150 cm
Mass of weight,
 = 20 kg
= 20 kg
Width, x = 4 cm
Distance d = 4 cm
Mass of bar,
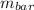 = 5 kg
= 5 kg
We are asked to find the center of mass from the mid-point,
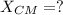
Since 3 weights are on the left and 2 weights are on the right, we know:
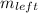 = 3 * 20 = 60 kg
= 3 * 20 = 60 kg
 = 2 * 20 = 40 kg
= 2 * 20 = 40 kg
And also we know that,
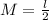 = 150/2 = 75 cm
= 150/2 = 75 cm
For the left side, center of mass is:
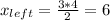 cm
cm
From the midpoint, the distance to the left is:
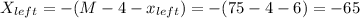 cm
cm
For the right side, center of mass is:
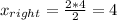 cm
cm
From the midpoint, the distance to the right will be:
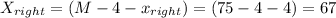 cm
cm
Hence,
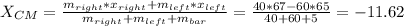 cm
cm