Question

A bakery wants to determine how many trays of doughnuts it should prepare each day. Demand is normal with a mean of 5 trays and standard deviation of 1 tray. If the owner wants a service level of at least 95%, how many trays should he prepare (rounded to the nearest whole tray)? Assume doughnuts have no salvage value after the day is complete. 6 5 4 7 unable to determine with the above information

Answer 1

P(3,7) = 0.95

He should prepare between 3 and 7 doughnuts

Explanation:

We need determine C such that

P(μ-c, μ+c) = 0.95

Where μ: Mean of doughnuts demands

For calculating C, we may use the table of the normal standard distribution

If P(μ-c, μ+c) = 0.95 by symetria P(μ+c) = 0.975, then

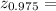`z_(0.975) =` (μ+c-μ)/δ

Where δ: Standard deviation

How
`z_(0.975) =` 1.96

1.96 =
`(c)/(1)`

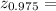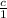
1.96 = c

Thus

P(3.04, 6.96) = 0.95

P(3,7) = 0.95

He should prepare between 3 and 7 doughnuts