Question

More on public university tuition. Construct a 95% confidence interval for the slope. What does this interval tell you about the annual percent increase in tuition between 2000 and 2008. what percent of the variability in 2008 tuition is explained by a linear regression model using the 2000 tuition

Answer 1

Answer: 95% Confidence interval: x±
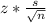`z*(s)/(√(n) )`. The R-squared value should tell us the percent of the variability explained by a linear regression

Explanation:

A 95% confidence interval will have to be constructed by adding and subtracting the z score or critical value for (in this case) a 95% confidence interval (typically would be 1.96) multiplied by the standard error which is
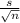`(s)/(√(n) )` where n is the sample size. Overall the general equation should look like: x±
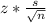`z*(s)/(√(n) )`. Adding to the given slope value would give the upper boundary of the confidence interval whereas deducting from the given slope value would give the lower boundary of the interval. This tells us that the true population parameter/slope should be contained within this interval 95% of the time when we run the sample multiple times or we are 95% certain that the true population parameter lies within these values. The R-squared value tells us the percentage of variability explained by a linear regression. We can observe this from the formula of the R-squared being the Explained Sum of Squares over/divided by the Total Sum of Squared