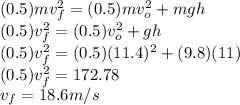Question

A hot-air balloon is 11.0 m above the ground and rising at a speed of 7.00 m/s. A ball is thrown horizontally from the balloon basket at a speed of 9.00 m/s. Ignore friction and air resistance and find the speed of the ball when it strikes the ground.

Answer 1

0.95 second

Step-by-step explanation:

height, h = 11 m

ux = 9 m/s

uy = 7 m/s

Let it takes time t to strike the ground.

Use second equation of motion

`h = u_(y)t + 0.5 gt^(2)`

- 11 = 7 t - 0.5 x 9.8 t²

-11 = 7t - 4.9t²

4.9t² - 7t - 11 = 0

`t=(-7\pm √(49+4*4.9*11))/(9.8)`

`t=(-7\pm 16.27)/(9.8)`

take positive sign

t = 0.95 second

Thus, the time taken to reach the ground is 0.95 second.

Answer 2

18.6 m/s

Step-by-step explanation:

`h` = Initial height of the balloon = 11 m

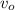`v_(o)` = initial speed of the ball

`v_(oy)` = initial vertical speed of the ball = 7 m/s

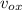`v_(ox)` = initial horizontal speed of the ball = 9 m/s

initial speed of the ball is given as

`v_(o) = \sqrt{v_(ox)^(2) + v_(oy)^(2)} = \sqrt{9^(2) + 7^(2)} = 11.4 m/s`

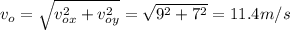
`v_(f)` = final speed of the ball as it strikes the ground

`m` = mass of the ball

Using conservation of energy

Final kinetic energy before striking the ground = Initial potential energy + Initial kinetic energy

`(0.5) m v_(f)^(2) = (0.5) m v_(o)^(2) + mgh \\(0.5) v_(f)^(2) = (0.5) v_(o)^(2) + gh\\(0.5) v_(f)^(2) = (0.5) (11.4)^(2) + (9.8)(11)\\(0.5) v_(f)^(2) = 172.78\\v_(f) = 18.6 m/s`