Question

A certain tennis player makes a successful first serve 6969​% of the time. Suppose the tennis player serves 9090 times in a match. ​a)​ What's the mean and standard deviation of the number of good first serves​ expected? ​b) Determine if you can use a normal model to approximate the distribution of the number of good first serves. ​c)​ What's the probability she makes at least 7272 first​ serves?

Answer 1

a) 4.387

b) Yes, because np & npq are greater than 10.

c) = 0.017

Explanation:

Give data:

p = 0.69

n = 90

a) a

E(X) = np = 62.1

`SD(X) = √((np(1-p)))`

`=√(90* 0.69(1- 0.69))`

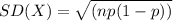
= 4.387

b)

np = 62.1

q = 1 - p = 1 - 0.69 = 0.31

npq = 19.251

Yes, because np & npq are greater than 10.

c.

`P(X \geq 72   ) = P(X > 71.5)` [continuity correction]

`=    P(Z> (((71.5-62.1))/( 4.387))`

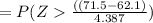
= P(Z> 2.14 )

= 1 - P(Z<2.14)

= 1 - 0.983 (using table)

= 0.017