Question

A drone traveling horizontally at 110 m/s over flat ground at an elevation of 3000 meters must drop an emergency package on a target on the ground. The trajectory of the package is given by x = 110 t , y = − 4.9 t 2 + 3000 , t ≥ 0 where the origin is the point on the ground directly beneath the drone at the moment of release. How many horizontal meters before the target should the package be released in order to hit the target? Round to the nearest meter.

Answer 1

The horizontal distance of the target should be 2721,4 meters.

Step-by-step explanation:

First of all we need to find the time that the emergency package hits the ground after the moment of release:

y=0 (because when it hits the ground it is on the level of 0m);

`0=-4,9*t^2+3000\\t=24,74`

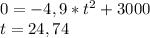
The emergency package hits the ground after 24,74 seconds from release.

Lets assume that package preserves his 110 m/s horizontal speed during the free fall. The targets horizontal distance is:

`110*24,74=2721,4`

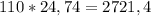
2721,4 meters