Question

On a very cold winter day, 5% of the production employees at CNC Cleaning Services, Inc. are absent from work. The production employees are randomly selected for a special in-depth study on absenteeism. Based on this data, what is the probability of randomly selecting 10 production employees on a cold winter day and finding that none of them are absent?

Answer 1

There is a 59.87% probability of randomly selecting 10 production employees on a cold winter day and finding that none of them are absent.

Explanation:

For each employee, there are only two possible outcomes. Either they are absent, or they are not. This means that we can solve this problem using the binomial probability distribution.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

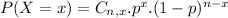
In which
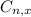`C_(n,x)` is the number of different combinatios of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

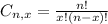
And p is the probability of X happening.

In this problem we have that:

`p = 0.05, n = 10`

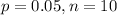
We want to find P(X = 0). So:

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(10,0).(0.05)^(0).(0.95)^(10) = 0.5987`

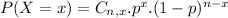
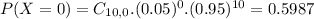
There is a 59.87% probability of randomly selecting 10 production employees on a cold winter day and finding that none of them are absent.