Question

A small object with an initial temperature of 135 degrees Fahrenheit is dropped into a tub with a temperature of 60 degrees Fahrenheit. The function f(t)=Ce(−kt)+60 represents the situation, where t is time in minutes, C is a constant, and k is a constant. After 6 minutes the object has a temperature of 85 degrees. What is the approximate value of k?

Answer 1

0.1831 s⁻¹

Step-by-step explanation:

Answer 2

0.1831 s⁻¹

Step-by-step explanation:

The function represents the temperature of the object at a certain time. Because there's a difference in temperature between the object and the tube, heat must flow from the object, and they will achieve thermal equilibrium.

At the beginning, t = 0, the temperature is 135°F, thus:

`135= C*e^(-k*0) + 60`

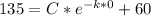
135 = C + 60

C = 75°F

After 6 minutes, t = 6, the temperature is 85°F, thus:

`85= 75*e^(-k*6) + 60`

`75*e^(-6k) = 25`

`e^(-6k) = 0.3333`

`ln(e^(-6k)) = ln(0.3333)`

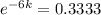
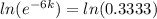
-6k = -1.0986

k = 0.1831 s⁻¹