Answer:
Reject H0 since test statistic <-2.492
Explanation:
Given that the American Water Works Association reports that the per capita water use in a single-family home is 74 gallons per day.
n = 25
x bar = 69
s= 8.3
std error = s/sqrt n =

H0:
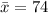
Ha:
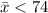
(Left tailed test at 5% significance level)
a) Reject H0 if t
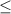 -2.492
-2.492
b) Test statistic = mean difference/std error
=
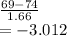
=-3.01
df =24
c) Reject H0