Question

On Melissa's 6th birthday, she gets a $2000 CD that earns 3% interest,

compounded semiannually. If the CD matures on her 13th birthday, how much

money will be available?

Answer 1

Using the formula for compound interest, the value of Melissa's $2000 CD, which earns 3% interest compounded semiannually, will be approximately $2463.20 when it matures on her 13th birthday after 7 years.

The subject of the question is mathematics, specifically dealing with the topic of compound interest. Melissa receives a certificate of deposit (CD) for $2000 that earns 3% interest compounded semiannually. Since compound interest is being used, we will apply the formula for compound interest which is
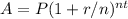`A = P(1 + r/n)^{nt`, where A is the amount of money accumulated after n years, including interest, P is the principal amount ($2000), r is the annual interest rate (3%), n is the number of times that interest is compounded per year (2 for semiannually), and t is the time the money is invested for in years.

Melissa's CD matures in 7 years (13 - 6), so we can calculate the final value of the CD as follows:

Firstly, convert the interest rate from a percentage to a decimal by dividing by 100:

3% / 100 = 0.03.

Plug in the values into the formula:

`A = 2000(1 + 0.03/2)^{2 * 7`.

Calculate the amount within the parentheses:

1 + 0.03/2

= 1.015.

Putting this value in the above equation,

`A=2000(1.015)^{14`

A=2463.20

Thus, the value of Melissa's CD, when it matures on her 13th birthday, will be approximately $2463.20.

Answer 2

$ 2463.51 will be available.

Explanation:

Since, the amount formula in compound interest,

`A = P(1+(r)/(n))^(nt)`

Where,

P = principal amount,

r = annual interest,

n = number of compounding periods,

t = number of years

We have,

P = $ 2000,

r = 3% = 0.03,

Number of years from 6th birthday to 13th birthday , t = 7 years,

n = 2 ( semiannual in a year ),

Hence, the final amount of CD,

`A=2000(1+(0.03)/(2))^(14)`

`= 2000(1+0.015)^(14)`

`=2000(1.015)^(14)`

`\approx \$ 2463.51`