Question

A plastic block of mass 0.20.2kg is initially at rest on a horizontal frictionless surface. A bullet of mass 1212 g is fired with an initial speed of 550550m/s towards the block. The bullet passes completely through the block and exits the other side with a speed of 20.020.0m/s. What percent of the initial kinetic energy of the bullet block system is lost during the collision?

Answer 1

94.29619%

Step-by-step explanation:

`m_1` = Mass of bullet= 0.012 kg

`m_2` = Mass of block = 0.2 kg

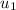`u_1` = Initial Velocity of bullet= 550 m/s

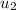`u_2` = Initial Velocity of block = 0 m/s

`v_1` = Final Velocity of bullet = 20 m/s

`v_2` = Final Velocity of block

As the linear momentum of the system is conserved

`m_1u_1+m_2u_2=m_1v_1+m_2v_2\\\Rightarrow v_2=(m_1u_1+m_2u_2-m_1v_1)/(m_2)\\\Rightarrow v_2=(0.012* 550+0.2* 0-0.012* 20)/(0.2)\\\Rightarrow v_2=31.8\ m/s`

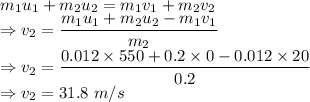
Change in kinetic energy is given by

`\Delta K=(1)/(2)(m_1u_1^2-m_1v_1^2-m_2v_2^2)\\\Rightarrow \Delta K=(1)/(2)(0.012* 550^2-0.012* 20^2-0.2* 31.8^2)\\\Rightarrow \Delta K=1711.476\ J`

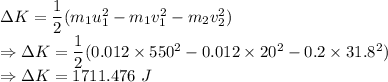
Percentage change is given by

`(\Delta K)/((1)/(2)m_1u_1^2)* 100=(1711.476)/((1)/(2)0.012* 550^2)* 100=94.29619\ \%`

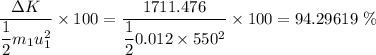
The percent of the initial kinetic energy of the bullet block system is lost during the collision is 94.29619%