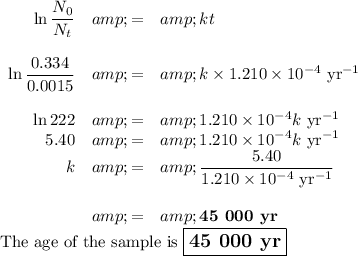Question

A sample has a C614 activity of 0.0015 Bq per gram of carbon.

(a) Find the age of the sample, assuming that the activity per gram of carbon in a living organism has been constant at a value of 0.23 Bq.
(b) Evidence suggests that the value of 0.23 Bq might have been as much as 45% larger. Repeat part (a), taking into account this 45% increase.

Answer 1

`\large \boxed{\text{(a) 42 000 yr;  (b) 45 000 yr}}`

Step-by-step explanation:

Two important equations in radioactive decay are

`\ln (N_(0) )/(N_(t)) = kt\\\\t_{(1)/(2)} = (\ln2)/(k )`

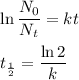
We use them for carbon dating.

(a) Initial activity = 0.23 Bq

(i) Calculate the rate constant

The half-life of ¹⁴C is 5730 yr.

`\begin{array}{rcl}t_{(1)/(2)}& = &(\ln2)/(k )\\\\k& = &\frac{\ln2}{t_{(1)/(2)}}\\\\ & = & \frac{\ln2}{\text{5730 yr}}\\\\ & = & 1.210 * 10^(-4)\text{ yr}^(-1)\\\end{array}`

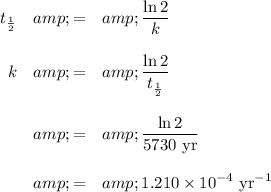
(ii) Calculate the age of the sample

`\begin{array}{rcl}\ln (N_(0) )/(N_(t)) & = & kt\\\\\ln (0.23 )/(0.0015) & = & k* 1.210 * 10^(-4)\text{ yr}^(-1)\\\\\ln 153 & = &  1.210 * 10^(-4)k \text{ yr}^(-1)\\5.03 & = & 1.210 * 10^(-4)k \text{ yr}^(-1)\\k & = & \frac{5.03}{1.210 * 10^(-4) \text{ yr}^(-1)}\\\\ & = & \textbf{42 000 yr}\\\end{array}\\\text{The age of the sample is $\large \boxed{\textbf{42 000 yr}}$}`

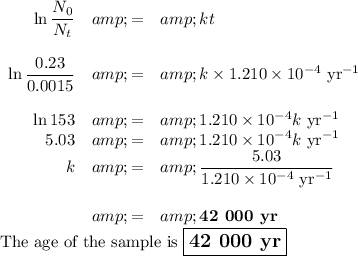
(b) Initial activity = 45 % larger

N₀ = 1.45 × 0.230 Bq = 0.334 Bq

`\begin{array}{rcl}\ln (N_(0) )/(N_(t)) & = & kt\\\\\ln (0.334 )/(0.0015) & = & k* 1.210 * 10^(-4)\text{ yr}^(-1)\\\\\ln 222 & = &  1.210 * 10^(-4)k \text{ yr}^(-1)\\5.40 & = & 1.210 * 10^(-4)k \text{ yr}^(-1)\\k & = & \frac{5.40}{1.210 * 10^(-4) \text{ yr}^(-1)}\\\\ & = & \textbf{45 000 yr}\\\end{array}\\\text{The age of the sample is $\large \boxed{\textbf{45 000 yr}}$}`