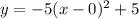Question

A parabolic arch needs to be 5m high and 2m wide at ground level. Find the quadratic equation which describes the arch.

Answer 1

`y=-5(x-0)^2+5`

Explanation:

Given height of parabola is
`5\ m`.

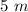And
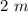`2\ m` wide at ground level.

Also, the parabola opens down.

Let us assume the parabola is aligned on Y-axis

As the height of parabola is
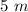`5\ m`. The maximum height of parabola is achieved when
`x=0`.

So, the vertex of parabola is
`(0,5)`.

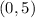The equation of parabola having vertex
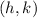`(h,k)` is.

`y=a(x-h)^2+k`.

Plugging the vertex of parabola

`(h,k)`
`=`
`(0,5)`.

`h=0\ and\ k=5`

`y=a(x-0)^2+5`

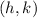
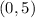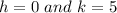
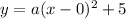
It is given that parabola is
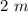`2\ m` wide at the ground.

As the parabola is aligned on Y-axis. So, distance between X-intercept is
`2\ m`.

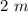The X-intercept would be
`(-1,0)\ and\ (1,0)`

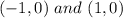
Plugging
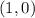`(1,0)` in the equation
`y=a(x-0)^2+5`

`0=a(1-0)^2+5\\\\-5=a(1)^2\\\\-5=a`

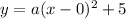
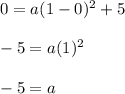
Now, we get
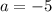`a=-5` and having vertex
`h=0\ and\ k=5`.

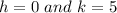So, the equation of parabola is

`y=a(x-h)^2+k`.

`y=-5(x-0)^2+5`