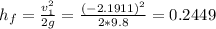Answer:
a) 5.2170 m/s
b) 2.1911 m/s, to the left
c) 3.0259 m/s, to the right
d) 0.2449 m
Step-by-step explanation:
Given parameters:
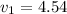
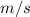
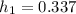


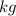
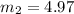
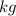
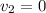
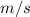
a) Here, the conservation of energy principle can be used.
 where
where
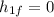
So,
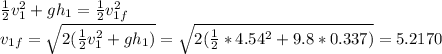
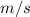
b) Here, the conservation of momentum principle can be used.

Here, our new
 will be
will be
 found in part (a).
found in part (a).

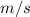
(-) sign means that the 2.03 kg ball after collision will bounce back in the left direction.
c) Here, we can use the conservation of momentum principle again.
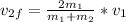 . Here,
. Here,
 will be
will be
 found in part (a) again.
found in part (a) again.

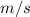
(+) sign means that the 4.97 kg ball after collision will swing to the right direction.
d) Here, we can use the conservation of energy principle again.
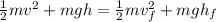 where
where
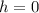 and
and
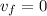
So,