Answer:

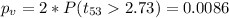
So with the p value obtained and using the significance level given
 we have
we have
 so we can conclude that we have enough evidence to reject the null hypothesis, and we can said that at 5% of significance the mean of the group 1 (Philadelphia) is significantly different than the mean for the group 2 (Baltimore).
so we can conclude that we have enough evidence to reject the null hypothesis, and we can said that at 5% of significance the mean of the group 1 (Philadelphia) is significantly different than the mean for the group 2 (Baltimore).
Explanation:
The system of hypothesis on this case are:
Null hypothesis:
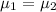
Alternative hypothesis:
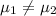
Or equivalently:
Null hypothesis:

Alternative hypothesis:
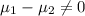
Our notation on this case :
 represent the sample size for group 1 (Philadelphia)
represent the sample size for group 1 (Philadelphia)
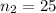 represent the sample size for group 2 (Baltimore)
represent the sample size for group 2 (Baltimore)
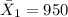 represent the sample mean for the group 1
represent the sample mean for the group 1
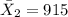 represent the sample mean for the group 2
represent the sample mean for the group 2
 represent the sample standard deviation for group 1
represent the sample standard deviation for group 1
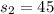 represent the sample standard deviation for group 2
represent the sample standard deviation for group 2
If we see the alternative hypothesis we see that we are conducting a bilateral test or two tail.
Critical values
On this case since the significance level is 0.05 and we are conducting a bilateral test we have two critical values, and we need on each tail of the distribution
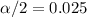 of the area.
of the area.
The distribution on this case since we don't know the population deviation for both samples is the t distribution with
 degrees of freedom.
degrees of freedom.
We can use the following excel codes in order to find the critical values:
"=T.INV(0.025,53)", "=T.INV(1-0.025,53)"
And we got: (-2.01, 2.01)
Calculate th statistic
The statistic is given by this formula:
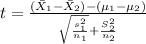
And now we can calculate the statistic:

The degrees of freedom are given by:
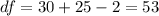
P value
And now we can calculate the p value using the altenative hypothesis:
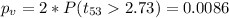
So with the p value obtained and using the significance level given
 we have
we have
 so we can conclude that we have enough evidence to reject the null hypothesis, and we can said that at 5% of significance the mean of the group 1 (Philadelphia) is significantly different than the mean for the group 2 (Baltimore).
so we can conclude that we have enough evidence to reject the null hypothesis, and we can said that at 5% of significance the mean of the group 1 (Philadelphia) is significantly different than the mean for the group 2 (Baltimore).