Question

Complete the explanation of how the figure illustrates that 6(9) = 6(4) + 6(5).

The area is the product of the length and width (6 × ? ). It is also the sum of the areas of the rectangles separated by the dished line (6 × ? and 6 × 5).
So, 6(9) = 6(4) + 6(5).

Answer 1

The explanation of how the figure illustrates that 6(9) = 6(4) + 6(5) is below.

`6* 9 = 6* 4 +6* 5`

Explanation:

Consider a Rectangle ABCD segregate in two Rectangle by a Dash Line

i.e Rectangle AEFD and

Rectangle EBCF

We Know

`\textrm{Area of Rectangle}=Length* Width`

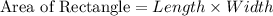
For Rectangle ABCD we have

Length = 6

Width = 9

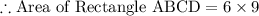`\therefore \textrm{Area of Rectangle ABCD}=6* 9`..........( 1 )

So For Rectangle AEFD we have

Length = 6

Width = 4

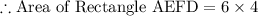`\therefore \textrm{Area of Rectangle AEFD}=6* 4`..........( 2 )

Similarly, For Rectangle EBCF we have

Length = 6

Width = 5

`\therefore \textrm{Area of Rectangle EBCF}=6* 5`..........( 3 )

Now,

`\textrm{Area of Rectangle ABCD}=\textrm{Area of Rectangle AEFD}+\textrm{Area of Rectangle EBCF}`

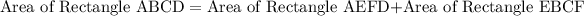
Substituting the values we get

`6* 9 = 6* 4 +6* 5`

Which is equal to

So, 6(9) = 6(4) + 6(5).