Question

A motel rents double rooms at $33 per day and single rooms at $27 per day. If 25 rooms were rented one day for a total of $771, how many rooms of each kind were rented?

Answer 1

Number of Single room rented = 9

Number of Double room rented = 16

Explanation:

Given:

Cost of motel rents for double rooms = $33 per day

Cost of motel rents for single rooms = $27 per day

Total number of rooms rented = 25

Cost of the 25 rooms = 771

To Find:

Number of double rooms and number of single rooms that were rented = ?

Solution:

Let

The number of Single rooms be x

The number of double rooms be y

total rooms rented = 25

x+ y = 25

x = 25 –y-------------------------------------------------------------(1)

Now the total cost

(Number of single rooms X Rent per single room) + (Number of double rooms X Rent per double room) = 771

`(x * 27) +( y * 33) = 771`-------------------------------------(2)

Substituting the value of (1) in (2), we get

`((25-y) * 27) +( y * 33) = 771`

675-27y+ 33y = 771

33y -27 y = 771-675

6y = 96

y =
`(96)/(6)`

y= 16-------------------------------------------------------------------------------(3)

Substituting (3) in (1)

x = 25 –16

x= 9

Answer 2

Number of single rooms rented is 9 and number of double rooms rented is 16

Solution:

Let "d" be the number of double rooms rented

Let "s" be the number of single rooms rented

Given that,

cost of double room per day = $ 33

cost of single room per day = $ 27

25 rooms were rented one day for a total of $771

We can frame a equation as:

number of single rooms rented + number of double rooms rented = 25

s + d = 25 --------- eqn 1

number of single rooms rented x cost of single room per day + number of double rooms rented x cost of double room per day = 771

`s * 27 + d * 33 = 771`

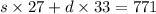
27s + 33d = 771 --------- eqn 2

Let us solve eqn 1 and eqn 2 to find values of "s" and "d"

From eqn 1,

s = 25 - d ------ eqn 3

Substitute eqn 3 in eqn 2

27(25 - d) + 33d = 771

675 - 27d + 33d = 771

675 + 6d = 771

6d = 771 - 675

6d = 96

d = 16

Substitute d = 16 in eqn 3

s = 25 - 16 = 9

s = 9

Thus number of single rooms rented is 9 and number of double rooms rented is 16