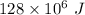Answer:
The kinetic energy of the airplane is
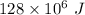
Step-by-step explanation:
Given:
Mass of the airplane is,
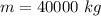
Velocity of the airplane is,
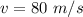
Height of airplane is,
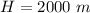
Kinetic energy of a body is independent of the height and only depends on its velocity.
Kinetic energy of a body of mass 'm' and moving with a velocity 'v' is given as:
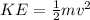
Where
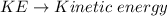
Now, plug in 40000 kg for 'm', 80 m/s for 'v' and solve for 'KE'. This gives,
![KE=(1)/(2)* (40000\ kg)* (80\ m/s)^2\\\\KE=20000* 6400\ kg\cdot m^2/s^2\\\\KE=128* 10^6\ J.....[1\ J=1\ kg\cdot m^2/s^2]](https://img.qammunity.org/2020/formulas/chemistry/middle-school/xdlnul4j9jhd8e0n5lzn4k87a1jpceniwx.png)
Therefore, the kinetic energy of the airplane is