Question

Which graph represents the solution to the given system ? Y=- 6X - 2Y +2=- 6X

Answer 1

Answer: The graph is attached.

Explanation:

The equation of the line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

Given the first equation:

`y=- 6x - 2`

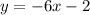
You can identify that:

`m=-6\\b=-2`

By definition, the line intersects the x-axis when
`y=0`. Then, subsituting this value into the equation and solving for "x", you get that the x-intercept is:

`0=- 6x - 2\\\\2=-6x\\\\x=-(1)/(3)\\\\x=-0.333`

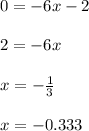
Now you can graph it.

Solve for "y" from the second equation:

`y +2=- 6x\\\\y=-6x-2`

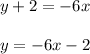
You can identify that:

`m=-6\\b=-2`

Notice that the slopes and the y-intercepts of the first line and the second line are equal; this means that they are exactly the same line and the System of equations has Infinitely many solutions.

See the graph attached.