Question

2. Juanita is trying to find the roots for the quadratic function f(x) = x2 + 64. She argues that there is no solution. Is Juanita correct? Justify your answer.

Answer 1

Yes, Juanita is correct.

Explanation:

Given:

The function given is:

`f(x)=x^2+64`

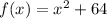
The roots of a function means the values of 'x' for which the function intersects or touches the x-axis. Therefore, the roots are nothing but the x-intercepts of the function.

In order to find the roots of the above function, we should equate it to 0.

So,
`f(x)=0`

`x^2+64=0\\\\x^2=-64`

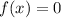
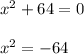
We know that, square of any number is always a positive quantity. But here, the square of 'x' is -64 which is a negative number. This is not possible.

So, there is no real solution to the given function. In other words, we can say that the function doesn't intersect the x-axis.

Therefore, Juanita is correct in her argument.