Question

A vector points -1.55 units along the x-axis and 3.22 units along the y-axis what is the magnitude of the vector

Answer 1

The magnitude of the vector is 3.57 units.

Step-by-step explanation:

The x component of the vector,
`v_x=-1.55\ \text{units}`

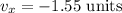
The y component of the vector is
`v_y=3.22\ \text{units}`

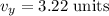
We need to find the magnitude of the vector. We know that the magnitude of the vector is given by :

`v=√(v_x^2+v_y^2)`

`v=√((-1.55)^2+(3.22)^2)`

`v=3.57\ \text{units}`

So, the magnitude of the vector is 3.57 units. Hence, this is the required solution.

Answer 2

3.57 units

Step-by-step explanation:

`x =√( (-1.55)^2+(3.22)^2) = 3.57 units`