Answer:
The product of 'x' and 'y' is
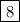 .
.
Explanation:
Given:
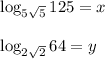
We need to determine the product of 'x' and 'y'.
Using the following logarithmic property:
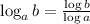
Here,
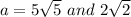
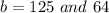
So,
![log_(5\sqrt5)125=(\log 125)/(\log 5√(5))\\\\log_(5\sqrt5)125=(\log 5^3)/(\log 5*5^(1/2)).......[\sqrt5=5^(1/2)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/iapb7ufj5xqypx875i63ow2ujvdr5jge52.png)
![log_(2\sqrt2)64=(\log 64)/(\log 2√(2))\\\\log_(2\sqrt2)64=(\log 2^6)/(\log 2*2^(1/2)).......[\sqrt2=2^(1/2)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/sruuwiuf85ghzpngnw0zl4afxldwaz5spb.png)
Now, we use another property of log and exponents.
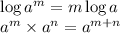
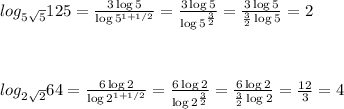
So,
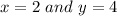
The product of 'x' and 'y' =
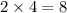
Therefore, the product of 'x' and 'y' is 8.