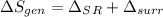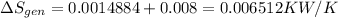Question

Refrigerant-134a enters a compressor as a saturated vapor at 160 kPa at a rate of 0.03 m3/s and leaves at 800 kPa. The power input to the compressor is 10 kW. If the surroundings at 20°C experience an entropy increase of 0.008 kW/K, determine (a) the rate of heat loss from the compressor, (b) the exit temperature of the refrigerant, and (c) the rate of entropy generation.

Answer 1

a)
`\dot Q_(out) = (20 + 273} * 0.008 = 2.344 kW`

b) T_2 = 36.4 degree C

c)
`\Delta S_(gen) = 0.006512 KW/K`

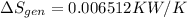
Step-by-step explanation:

Given data:

`P_1 = 160 kPa`

volumetric flow
`V_1 = 0.03 m^3/s`

`P_2 = 800 kPa`

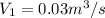
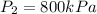
power input
`W_(in) = 10 kW`

`T_(surr) = 20 degree C`

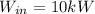
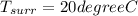
entropy = 0.008 kW/K

from refrigerant table for P_1 = 160 kPa and x_1 = 1.0

`v_1 = 0.12355 m^3/kg`

`h_1 = 241.14 kJ/kg`

`s_1 = 0.94202 kJ/kg K`

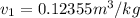
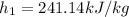
a) mass flow rate
`\dot m = (V_1)/(v_1)`

`\dot m = (0.03)/(0.12355) = 0.2428 kg/s`

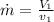
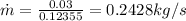
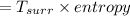
heat loss
`= T_(surr) * entropy`

heat loss
`\dot Q_(out) = (20 + 273} * 0.008 = 2.344 kW`

b) from energy balance equation

`W_(in) 0 \dot Q_(out) = \dot m (h_2 -h_1}`

`10 - 2.344 = 0.2428 (h_2 - 241.14}`

`h_2 = 272.67 kJ/kg`

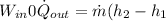
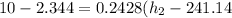
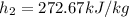
from refrigerant table, for P_2 = 800 kPa and h_2 = 272.67 kJ/kg

T_2 = 36.4 degree C

c) from refrigerant table P_2 = 800 kPa and h_2 = 272.67 kJ /kg

`s_2 = 0.93589 kJ/kg K`

rate of entropy

`\Delta S_R =  \dot m =(s_2 -s_1)`

`\Delta S_R = 0.2428 * (0.93589 -0.94202) = - 0.0014884 kW/K`

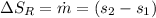
rate of entropy for entire process

`\Delta S_(gen) = \Delta _S_R + \Delta_(surr)`

`\Delta S_(gen) = 0.0014884 + 0.008 = 0.006512 KW/K`