Question

How much pressure is exerted by an 100n man with a shoe area of O.05cm square

​

Answer 1

Pressure = 20 MPa

Step-by-step explanation:

Given:

Force acting on the shoe is,
`F=100\ N`

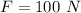
Area of shoe on which the force acts is,
`A= 0.05\ cm^2`

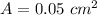
Now, first we convert the area into its standard unit of m².

We have the conversion factor as:

1 cm² =
`10^(-4)\ m^2`

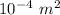
Therefore, the area of shoe in square meters is given as:

`A=0.05* 10^(-4)\ m^2\\A=5* 10^(-6)\ m^2`

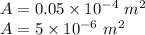
Now, pressure on the shoe is given as:

`P=(Force)/(Area)\\P=(F)/(A)`

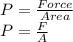
Plug in 100 N for 'F',
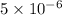`5* 10^(-6)` for 'A' and solve for 'P'. This gives,

`P=(100\ N)/(5* 10^(-6)\ m^2)\\P=20* 10^(6)\ N/m^2`

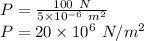
Now, we know that,

`10^(6)\ N/m^2=1\ MPa\\\therefore 20* 10^(6)\ N/m^2=20* 1\ MPa=20\ MPa`

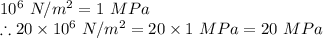
Therefore, the pressure acting on the shoe is 20 MPa.