Question

4 adult and 10 student tickets cost 58$ overall on the first day on the second 5 adult and 1 student cost 38$ overall how much is each ticket sold for

Answer 1

Cost of 1 adult ticket is $ 7 and cost of 1 student ticket is $ 3

Solution:

Let "a" be the cost of 1 adult ticket

Let "s" be the cost of 1 student ticket

Given that,

4 adult and 10 student tickets cost 58$ overall on the first day

So we can frame a equation as:

4 adult ticket x cost of 1 adult ticket + 10 student ticket x cost of 1 student ticket = $ 58

`4 * a + 10 * s = 58`

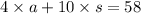
4a + 10s = 58 ------ eqn 1

On the second 5 adult and 1 student cost 38$ overall

So we can frame a equation as:

5 adult ticket x cost of 1 adult ticket + 1 student ticket x cost of 1 student ticket = $ 38

`5 * a + 1 * s = 38`

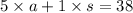
5a + 1s = 38 ------- eqn 2

Let us solve eqn 1 and eqn 2 to find values of "a" and "s"

Multiply eqn 2 by 10

50a + 10s = 380 ---- eqn 3

Subtract eqn 1 from eqn 3

50a + 10s = 380

4a + 10s = 58

( - ) --------------------

46a = 322

a = 7

Substitute a = 7 in eqn 1

4a + 10s = 58

4(7) + 10s = 58

28 + 10s = 58

10s = 58 - 28

10s = 30

s = 3

Thus cost of 1 adult ticket is $ 7 and cost of 1 student ticket is $ 3