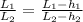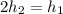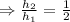Question

Two cylinders with the same mass density rhoC = 713 kg / m3 are floating in a container of water (with mass density rhoW = 1025 kg / m3). Cylinder #1 has a length of L1 = 20 cm and radius r1 = 5 cm. Cylinder #2 has a length of L2 = 10 cm and radius r2 = 10 cm. If h1 and h2 are the heights that these cylinders stick out above the water, what is the ratio of the height of Cylinder #2 above the water to the height of Cylinder #1 above the water (h2 / h1)? h2 / h1 =

Answer 1

Step-by-step explanation:

Given

density of cylinder is
`\rho _c=713 kg/m^3`

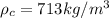
Length of first cylinder is
`L_1=20 cm`

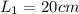
radius
`r_1=5 cm`

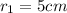
For cylinder 2
`L_2=10 cm`

`r_2=10 cm`

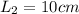
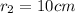
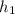`h_1` and
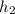`h_2` are the height above water

E

as object is floating so its weight must be balanced with buoyant force

`\rho _c(\pi )/(4)d_1^2L_1g=\rho _w(\pi )/(4)d_1^2(L_1-h_1)g----1`

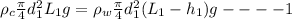
For 2nd cylinder

`\rho _c(\pi )/(4)d_2^2L_2g=\rho _w(\pi )/(4)d_2^2(L_2-h_2)g----2`

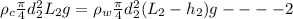
Dividing 1 and 2 we get

`(L_1)/(L_2)=(L_1-h_1)/(L_2-h_2)`

`(20)/(10)=(20-h_1)/(10-h_2)`

`2h_2=h_1`

`\\\Rightarrow(h_2)/(h_1)=(1)/(2)`