Answer:
The area of Triangle B is twice the area of Triangle A .
Explanation:
Given as :
Triangle A and Triangle B have same base
The height of Triangle A twice Triangle B
For Triangle A
The base of Triangle A =
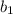 = b
= b
The height of Triangle A =
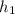 = h
= h
Let The area of Triangle A =
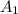
∵ The Area of Triangle =
 × base × height
× base × height
So,
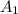 =
=
 × b × h ......1
× b × h ......1
For Triangle B
The base of Triangle B =
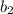 = b
= b
The height of Triangle B =
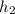 = twice the height of Triangle A
= twice the height of Triangle A
I.e
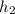 = 2 h
= 2 h
Let The area of Triangle B =

So,
 =
=
 × b × 2 h ........2
× b × 2 h ........2
Now, Comparing both equation 1 and 2
∵
 =
=
 × b × 2 h
× b × 2 h
Or,
 = 2 ×
= 2 ×
 × b × h
× b × h
Or,
 = 2 ×
= 2 ×
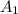
So, The area of Triangle B = 2 times The area of Triangle A
Hence, The area of Triangle B is twice the area of Triangle A . Answer