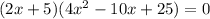Answer:
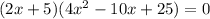
Explanation:
Given:
The given equation is.
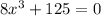
Find the some of cube.
Solution:
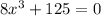
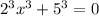
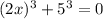 ----------(1)
----------(1)
The sum of the cube formula is given below.
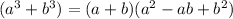 -----------(2)
-----------(2)
By comparing equation 1 and equation 2
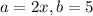
substitute a and b value in equation 2
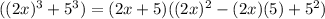
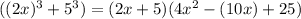
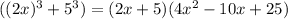
Therefore the sum of the cube