Question

As a way of determining the inductance of a coil used in a research project, a student first connects the coil to a 9.7 V battery and measures a current of 0.742 A. The student then connects the coil to a 27.3 V(rms), 51.1 Hz generator and measures an rms current of 0.429 A. What is the inductance?

Answer 1

L = 0.194 H

Step-by-step explanation:

given,

Voltage = 9.7 V

current = 0.742 A

R = 9.7 V / 0.742 A

R = 13.07 Ohms.

the A.C. impedance of the inductor, like this:

Z = V / I

Z = 27.3 V / 0.429 A

Z = 63.64 Ohms.

now,

inductive reactance, X_L

`X_L = √(Z^2 - R^2)`

`X_L = √(63.64^2 - 13.07^2)`

`X_L =62.28\ \Omega`

`X_L = 2\pi f * L`

`L = (X_L)/(2\pi f)`

`L = (62.28)/(2\pi * 51.1)`

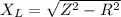
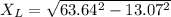
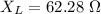
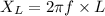
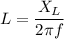
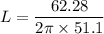
L = 0.194 H