Question

The curve given by the parametric equations;

x=36−t^2, y=t^3−25t
is symmetric about the x-axis. (If t gives us the point (x,y), then −t will give (x,−y) ).
a. At which x value is the tangent to this curve horizontal?
b. At which t value is the tangent to this curve vertical?

Answer 1

x=36, t = ±5/sqrt 3

Explanation:

we are given a curve reprsented by parametric equations.

`x=36-t^2,\\ y=t^3-25t`

Also given that this is symmetric about x axis.

For finding a tangent we first find slope i.e. dy/dx

If dy/dx has dy/dt in numerator and dx/dt in the denominator

Hence for a tangent to be horizontal slope =0

i.e.dy/dt =0

Similarly for a tangent to be vertical slope=undefined

Or dx/dt =0

a)
`(dx)/(dt) =-2t =0\\t=0\\x=36`

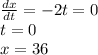
when x= 36, the tangent is horizontal

b)
`(dy)/(dt) =0\\3t^2-25 =-\\t=(5)/(√(3) ) ,-frac{5}{√(3) }`

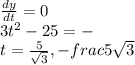
For these t values tangent is vertical.