Question

In​ 2000, the population of a country was approximately 5.77 million and by 2077 it is projected to grow to 13 million. Use the exponential growth model
`l_A = A_oe^(kt)`​, in which t is the number of years after 2000 and
`A_0` is in​ millions, to find an exponential growth function that models the data.

In which year will Israel's population be 12 million?

Answer 1

Part 1 :
`I_A = 5.77 e^(0.01055t)`

Part 2 : In 2069 the population would be 12 millions.

Explanation:

Part 1 : Given function that shows the population( in millions ) of Israel after t years since 2000,

`I_A = A_0 e^(kt)`

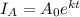
If t = 0,

`I_A = 5.77`

`\implies 5.77 = A_0 e^(0)\implies A_0 = 5.77`

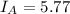
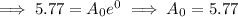
If t = 77 years,

The population in 2077,

`I_A = A_0 e^(77k)=5.77 e^(77k)`

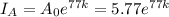
According to the question,

Population in 2077 = 13 millions

`13 = 5.77 e^(77k)`

`(13)/(5.77) = e^(77k)`

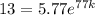
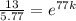
Taking ln both sides,

`\ln((13)/(5.77)) = \ln(e^(77k))`

`\ln((13)/(5.77)) = 77k`

`\implies k = 0.010549\approx 0.01055`

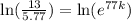
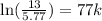
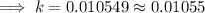
Hence, the required function would be,

`I_A = 5.77 e^(0.01055t)`

Part 2 : If
`I_A = 12`

`12 = 5.77 e^(0.01055t)`

`(12)/(5.77) = e^(0.01055t)`

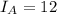
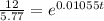
Taking ln both sides,

`\ln((12)/(5.77)) = \ln(e^(0.01055t))`

`\ln((12)/(5.77)) =0.01055t`

`\implies t\approx 69`

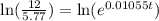
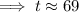
∵ 2000 + 69 = 2069

Hence, in 2069 the population would be 12 millions.