Question

Consider the situation when almost all of the magnetic moments of a sample of a particular ferromagnetic metal are aligned. In this case, the magnetic field can be calculated as the permeability constant μ0 multiplied by the magnetic moment per unit volume. In a sample of iron, for example, where the number density of atoms is approximately 8.50 ✕ 1028 atoms/m3, the magnetic field can reach 1.99 T. If each electron contributes a magnetic moment of 9.27 ✕ 10−24 A · m2 (1 Bohr magneton), how many electrons per atom contribute to the saturated field of iron?

Answer 1

2.00976

Step-by-step explanation:

B = Magnetic field = 1.99 T

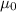`\mu_0` = Vacuum permeability =
`4\pi * 10^(-7)\ H/m`

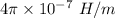
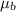`\mu_b` = Magnetic moment of each electron =
`9.27* 10^(-24)\ Am^2`

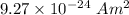
n = Number density of atoms =
`8.5* 10^(28)\ atoms/m^3`

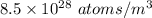
N = Number of electrons per atom

Magnetic field is given by

`B=N\mu_0\mu_bn\\\Rightarrow N=(B)/(\mu_0\mu_bn)\\\Rightarrow N=(1.99)/(4\pi* 10^(-7)* 9.27* 10^(-24)* 8.5* 10^(28))\\\Rightarrow N=2.00976`

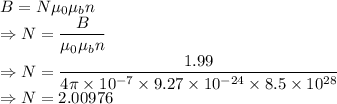
The number of electrons per atom contribute to the saturated field of iron is 2.00976