Question

Suppose a change of coordinates T:R2→R2 from the uv-plane to the xy-plane is given by x=4v−2u−3, y=−1+5u+4v.

(a) Find the absolute value of the determinant of the Jacobian for this change of coordinates. ∣∣∂(x,y)/∂(u,v)∣∣= ∣det |=



(b) If a region D∗ in the uv-plane has area 7.04, find the area of the region T(D∗) in the xy-plane. Area =

Answer 1

a) ∣∣∂(x,y)/∂(u,v)∣∣ = 28

b)Area = 197.12

Explanation:

a) Find the absolute value of the determinant of the Jacobian

Change of coordinates

x = 4v -2u-3

`(dx)/(du) = -2`

`(dx)/(dv) = 4`

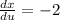
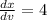
y = -1+5u+4v

`(dy)/(du) = 5`

`(dy)/(dv) = 4`

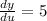
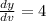
Then

∣∣∂(x,y)/∂(u,v)∣∣=∣det | =|
`\[ \begin{array}{cc}-2 & 4 \\ 5 & 4\end{array} \]`|

∣∣∂(x,y)/∂(u,v)∣∣ = ∣(-2)(4)-(5)(4)∣ = 28

b) The area of the region in the xy -plane is the area of the region in the uv-plane multiplies by the absolute value of the determinant of the Jacobian.

Thus

Area = (7.04)(28)

Area = 197.12