Question

Water flows at the rate of 5 m per minute through a cylindrical pipe, whose diameter is 7 cm. How long it will take to fill the conical vessel having base diameter 21 m and depth 12 m?

Answer 1

It will take 1200 hrs to fill the vessel.

Explanation:

Given:

diameter of the base of the conical vessel = 21 m

radius of the base of the conical vessel r =
`(21)/(2)\ m`

height of the conical vessel = 12 m

Now we know the formula of Volume of conical vessel

volume of the conical vessel =
`(1)/(3) \pi r^2h`

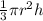
Substituting the values we get;

volume of the conical vessel =
`(1)/(3) * \pi *(21)/(2) * (21)/(2) *12 \ \ \ \ \ equation\ 1`

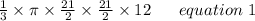
Also Given:

Diameter of Cylindrical pipe = 7 cm

Radius of Cylindrical pipe =
`(7)/(2) \ cm`

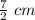
Now we know that 1 cm = 0.01 m

Hence Radius of Cylindrical pipe =
`(7)/(200) \ m`

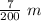
Let the conical vessel is filled in x minutes.

Then, length if the water column =
`5x\ m`

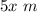
Hence water column forms a cylinder of length
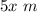`5x\ m` and radius
`(7)/(200) \ m`

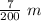
So, Volume of water that flows in x minutes is given by =
`\pi r^2h`

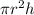
Volume of Water that flows in x minutes =
`\pi * (7)/(200) * (7)/(200) * 5x`

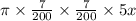
We will find the value of x by saying volume of the conical vessel is equal to Volume of Water that flows in x minutes.

Hence,

`(1)/(3) * \pi *(21)/(2) * (21)/(2) *12 = \pi * (7)/(200) * (7)/(200) * 5x`

`x=72000\ mins`

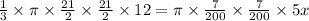
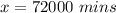
Since 1 hour = 60 min

`x = (72000)/(60)= 1200 \ hrs`

Hence it will take 1200 hrs to fill the vessel.