Answer:
It is going to be bell-shaped(normally distributed), with mean
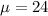 and standard deviation
and standard deviation
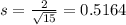 .
.
Explanation:
The Central Limit Theorem estabilishes that, for a random variable X, with mean
 and standard deviation
and standard deviation
 , a large sample size can be approximated to a normal distribution with mean
, a large sample size can be approximated to a normal distribution with mean
 and standard deviation
and standard deviation
 .
.
What can we say about the shape of the distribution of the sample mean time?
It is going to be bell-shaped(normally distributed), with mean
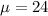 and standard deviation
and standard deviation
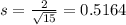 .
.