Answer:
The Area of Δ DFG is 175 cm²
The Area of Δ ABC is 252 cm²
Explanation:
Given as :
The Δ ABC is similar to the Δ DFG
The area of the triangle ABC is greater than the area of the triangle DFG by 77 cm²
Let The area of Δ DFG = x cm²
So, The area of Δ ABC = ( 77 + x ) cm²
The ratio of corresponding sides of Δ ABC and Δ DEF = 6 : 5
Let The side AB = 6 y
And The side DE = 5 y
Now, from The property of similar Triangles
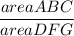 =
=

I.e
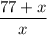 =
=
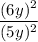
Or,
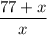 =
=
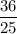
Or, 25 × (77 + x ) = 36 x
Or, 25 × 77 + 25 x = 36 x
Or, 25 × 77 = 36 x - 25 x
Or, 11 x = 25 × 77
∴ x =
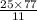
I.e x = 175 cm²
So,The Area of Δ DFG = x = 175 cm²
And The Area of Δ ABC = x + 77 = 175 + 77 = 252 cm²
Hence, The Area of Δ DFG is 175 cm²
And The Area of Δ ABC is 252 cm² Answer