Answer:
0.624 is the probability that a randomly selected college student will take between 2 and 6 minutes to find a parking spot in the main parking lot.
Explanation:
We are given the following information in the question:
Mean, μ = 5 minutes
Standard Deviation, σ = 2 minutes
We are given that the distribution of time is a bell shaped distribution that is a normal distribution.
Formula:
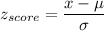
P(student will take between 2 and 6 minutes )

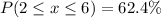
0.624 is the probability that a randomly selected college student will take between 2 and 6 minutes to find a parking spot in the main parking lot.