Answer:
The sprinkler must rotate by an angle of 107.48°.
Explanation:
Given:
Area of strawberry patch( in shape of sector) = 1500 square yards
Radius of circle = 40 yards
To find angle through which the sprinkler should rotate.
Solution.
In order to find the angle of rotation of sprinkler, we will apply the area of sector formula.
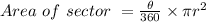
where
 is the angle of the sector formed and
is the angle of the sector formed and
 is radius of the circle.
is radius of the circle.
Thus, we can plugin the given values to find
 which would be the angle of rotation.
which would be the angle of rotation.
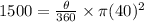
Taking
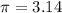
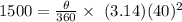
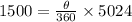
Dividing both sides by 5024.
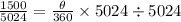
Multiplying both sides by 360.
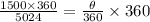
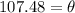
∴
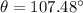
Angle of rotation of sprinkler = 107.48°