Answer:
FV = 2762.07
Explanation:
Use the equation for amount after compound interest
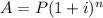
"A" is the amount, same as future value, like the total
"P" is the principal, the starting amount or initial investment or loan
"i" is the interest rate earned each compounding period, in decimal form
"n" is the number of compounding periods
A = ?
P = 2500
The interest rate is calculated by dividing the annual interest rate in decimal form by the compounding frequency (how many times interest is calculated each year)
i = r/c
Find "r". The annual interest rate is 2,5%. To convert it to decimal form, divide it by 100.
r = 2,5% = 0.025
"c" is the compounding frequency. The problem states "compounded quarterly", meaning 4 times a year.
c = 4
Substitute r and c into the formula
i = r/c
i = 0.025/4
i = 0.00625
The number of compounding periods is calculated by multiplying the time in years by the compounding frequency (how many times interest is calculated each year)
n = tc
The problem states it was compounded for "4 years".
t = 4
It was compounded quarterly.
c = 4
Substitute c and t into the formula
n = tc
n = (4)(4)
n = 16
Now that we know all of the variables' values except for one, we can solve for the missing variable, "A", future value.
Substitute P, i, and n into the formula:
A = P(1+i)ⁿ
A = 2500(1+0.00625)¹⁶ Solve inside the brackets
A = 2500(1.00625)¹⁶ Enter into calculator. Do the exponent first, then multiply by 2500.
A = 2762.07 Answer, rounded off to two decimal places
Since A = FV, the future value is ₴2762.07.