Answer:
a) The 99% confidence interval would be given (0.503;0.557).
We are 99% confident that this interval contains the true population proportion.
b)
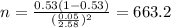
And rounded up we have that n=664
Explanation:
Data given and notation
n=2343 represent the random sample taken
X represent the people that they have watched digitally streamed TV programming on some type of device
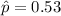 estimated proportion of people that they have watched digitally streamed TV programming on some type of device
estimated proportion of people that they have watched digitally streamed TV programming on some type of device
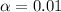 represent the significance level
represent the significance level
Confidence =0.99 or 99%
z would represent the statistic for the confidence interval
p= population proportion of people that they have watched digitally streamed TV programming on some type of device
The population proportion present the following distribution:

Part a) Confidence interval
The confidence interval would be given by this formula
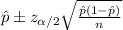
For the 99% confidence interval the value of
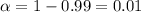 and
and
 , with that value we can find the quantile required for the interval in the normal standard distribution.
, with that value we can find the quantile required for the interval in the normal standard distribution.

And replacing into the confidence interval formula we got:
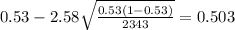
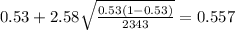
And the 99% confidence interval would be given (0.503;0.557).
We are 99% confident that this interval contains the true population proportion.
Part b) What sample size would be required for the width of a 99% CI to be at most 0.05 irrespective of the value of p??
The margin of error for the proportion interval is given by this formula:
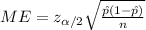 (a)
(a)
And on this case we have that
 and we are interested in order to find the value of n, if we solve n from equation (a) we got:
and we are interested in order to find the value of n, if we solve n from equation (a) we got:
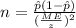 (b)
(b)
And replacing into equation (b) the values from part a we got:
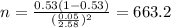
And rounded up we have that n=664