Answer:
The area of triangles are 16 cm^2 and 49 cm^2
Explanation:
we know that
If two figures are similar, the ratio of its perimeters is equal to the scale factor and the ratio of its areas is equal to the scale factor squared
Let
z ----> the scale factor
x ----> the area of the smaller triangle in square centimeters
y ----> the area of the larger triangle in square centimeters
we know that
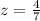
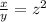
so
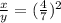
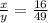
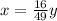 -----> equation A
-----> equation A
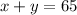 ----> equation B
----> equation B
solve the system by substitution
substitute equation A in equation B
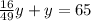
solve for y
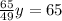
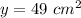
Find the value of x


therefore
The area of triangles are 16 cm^2 and 49 cm^2