Question

Exhibit B In order to determine whether or not there is a significant difference between the hourly wages of two companies, two independent random samples were selected and the following statistics were calculated. Company A Company B Sample size 80 60 Sample mean $6.75 $6.25 Population standard deviation $1.00 $0.95 Refer to Exhibit B. The value of the test statistic is _____.

a. 2.75
b. 0.098
c. 3.01
d. 1.645

Answer 1

Answer: c. 3.01

Explanation:

The test statistic for difference between two population mean (when population standard deviation is known) is given by :

`z=\frac{\overline{x}_1-\overline{x}_2}{\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}}`

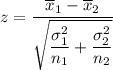
, where
`n_1` = Size of first sample

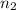`n_2` = Size of second sample

`\overline{x}_1-\overline{x}_2` = Difference between two sample mean.

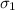`\sigma_1` = standard deviation for population 1.

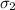`\sigma_2` = standard deviation for population 2.

As per given , we have

`n_1=80`

`n_2=60`

`\overline{x}_1=\$6.75`

`\overline{x}_2=\$6.25`

`\sigma_1=\$1`

`\sigma_2=\$0.95`

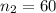
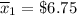
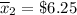
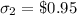
Substitute these values in formula , we get

`z=\frac{6.75-6.25}{\sqrt{((1)^2)/(80)+((0.95)^2)/(60)}}`

`z=(0.50)/(√(0.0275416666667))`

`z=(0.50)/(0.165956821694)`

`z=3.0128318613\approx3.01`

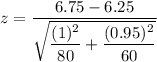
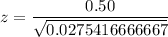
Hence, the value of the test statistic is 3.01.

Hence, the correct option is c. 3.01 .