Question

The demand equation for a monopolistic firm’s product is 4p+q= 320, and the firm’s cost function is given by c = 0.1q2+ 10q+ 1500. Find the price that maximizes the firm’s profit. What is the firm’s profit?

Answer 1

price =100 and profit is $2000

Explanation:

The demand equation for a monopolistic firm’s product is 4p+q= 320

Solve for p

`4p+q= 320`

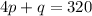
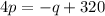`4p=-q+320`, divide both sides by 4

`p=-(q)/(4)+80`

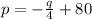
Revenue function R= p times q

`R=p \cdot q=-(q^2)/(4)+80q`

`C= 0.1q^2+ 10q+ 1500`

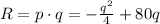
Profit = Revenue - Cost

`Profit=-(q^2)/(4)+80q-(0.1q^2+ 10q+ 1500)`

`Profit P(q)=-0.35q^2+70q-1500`

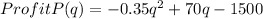
to find maximum profit find out vertex

`q=(-b)/(2a) =(-70)/(2(0.35)) =100`

Plug in 100 for q inf P(q)

`Profit P(100)=-0.35(100)^2+70(100)-1500=2000`

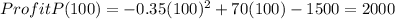
price =100 and profit is $2000