Answer: NO.
Explanation:
As per given , we have to test the hypothesis.
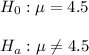
∵
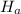 is two-tailed , so our test is a two-tailed test.
is two-tailed , so our test is a two-tailed test.
Also, the standard deviation is known to be 0.8 , so we use z-test.
Test statistic:
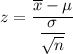
, where
 = Sample mean
= Sample mean
 = population mean
= population mean
 = Population standard deviation
= Population standard deviation
n= Sample size
Put



n= 110 , we get
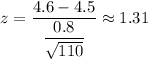
P-value for two tailed test = 2P(Z>|z|)
= 2P(Z>|1.31|) = 2(1-P(Z<1.31)) [∵ P(Z>z)=1-P(Z<z)]
=2(1- 0.9049) [By z-table]
=0.1902
Decision : ∵ P-value (0.1902) > Significance level (0.02).
It means we do not reject the null hypothesis.
[When P-values < Significance level then we reject the null hypothesis.]
Conclusion : We do not have sufficient evidence at the 0.02 level that the valve does not perform to the specifications.