Answer:
16, 20, 24, 28, and 32
Explanation:
Given:
The
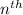 term of the sequence is given as:
term of the sequence is given as:
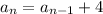
The first term is given as
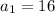
We need to find the remaining 4 terms.
So, we plug in 2, 3, 4, 5 for 'n' and find the remaining 4 terms of the sequence.
For
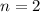
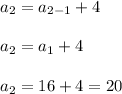
For
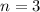
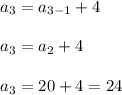
For
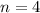
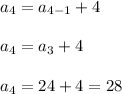
For
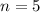
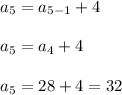
Therefore, the first five terms of the given sequence are:
16, 20, 24, 28, and 32