Question

A flat uniform circular disk has a mass of 3.97 kg and a radius of 85.7 cm. It is suspended in a horizontal plane by a vertical wire attached to its center. If the disk is rotated 2.42 rad about the wire, a torque of 0.0688 N·m is required to maintain that orientation. Calculate

(a) the rotational inertia of the disk about the wire,
(b) the torsion constant, and
(c) the angular frequency of this torsion pendulum when it is set oscillating.

Answer 1

1.457881265 kgm²

0.02842 Nm/rad

0.13962 rad/s

Step-by-step explanation:

M = Mass = 3.97 kg

R = Radius = 85.7 cm

`\tau` = Torque = 0.0688 Nm

`\theta` = Angle of rotation = 2.42 rad

Moment of inertia about the center of the disk is given by

`I=(1)/(2)MR^2\\\Rightarrow I=(1)/(2)* 3.97* 0.857^2\\\Rightarrow I=1.457881265\ kgm^2`

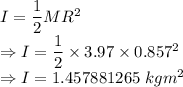
The rotational inertia of the disk about the wire is 1.457881265 kgm²

Torque is given by

`\tau=\kappa \theta\\\Rightarrow \kappa=(\tau)/(\theta)\\\Rightarrow \kappa=(0.0688)/(2.42)\\\Rightarrow \kappa=0.02842\ Nm/rad`

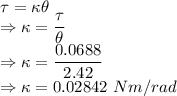
The torsion constant is 0.02842 Nm/rad

Time period is given by

`T=2\pi\sqrt{(I)/(\kappa)}`

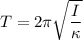
Angular frequency is given by

`\omega=(2\pi)/(T)\\\Rightarrow \omega=\sqrt{(\kappa)/(I)}\\\Rightarrow \omega=\sqrt{(0.02842)/(1.457881265)}\\\Rightarrow \omega=0.13962\ rad/s`

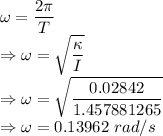
The angular frequency of this torsion pendulum when it is set oscillating is 0.13962 rad/s